HYGENE: A Diffusion-based Hypergraph Generation Method

This blog post will summarize our paper, HYGENE: A Diffusion-based Hypergraph Generation Method, accepted at AAAI-25. To the best of our knowledge, this work introduces the first deep-learning based method for hypergraph generation. Code is available here.

TL;DR: We introduce a hypergraph generation method based on an “unzoom-zoom” principle. First, we compute increasingly coarse versions of a hypergraph (“unzoom”). Then, we train a model to reconstruct the original details from these simplified versions (“zoom”). To simplify processing, we project hypergraphs into graph space using two different projections, each preserving specific characteristics. Generation is achieved by repeatedly applying the trained model to zoom in, gradually increasing detail until the desired hypergraph size is reached.

Preliminaries

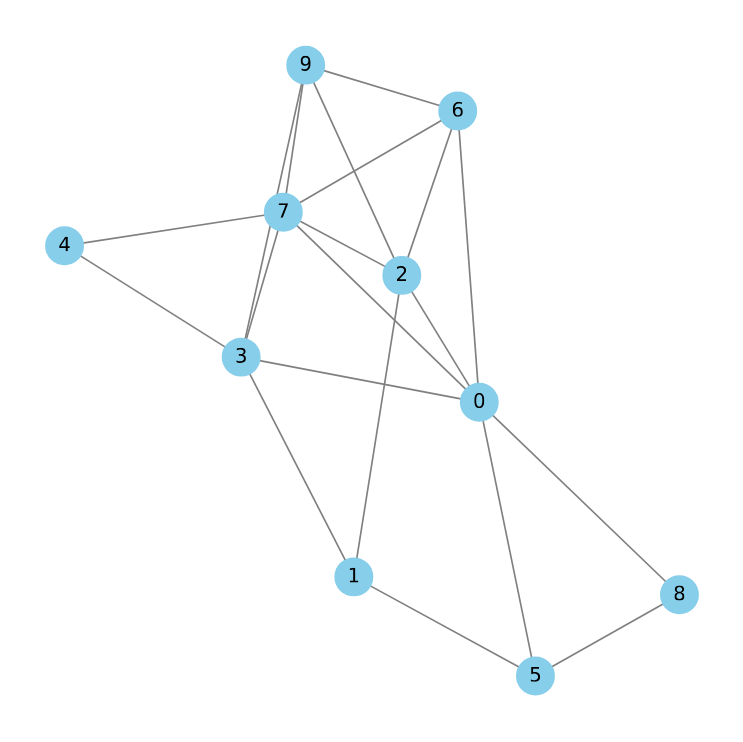
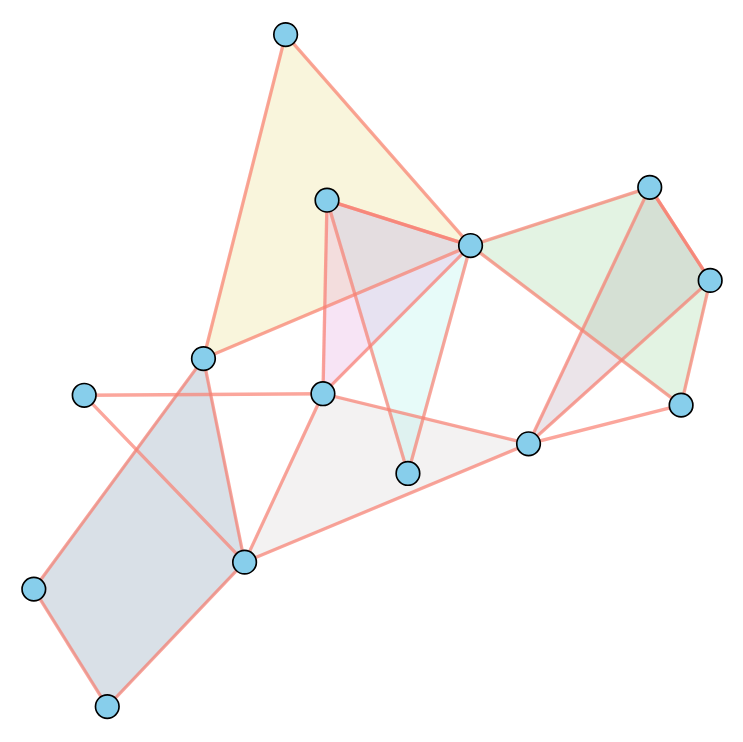
A random graph and a random hypergraph.

Traditional graphs consist of nodes connected by edges, with each edge linking precisely two nodes. Hypergraphs, however, offer a more versatile framework. In a hypergraph, edges — referred to as hyperedges — can connect an arbitrary number of nodes simultaneously. This generalization allows hypergraphs to capture higher-order and more nuanced relationships compared to standard graphs. This also makes them much more expressive, for instance:

3D meshes can be represented with triangles as 3-edges
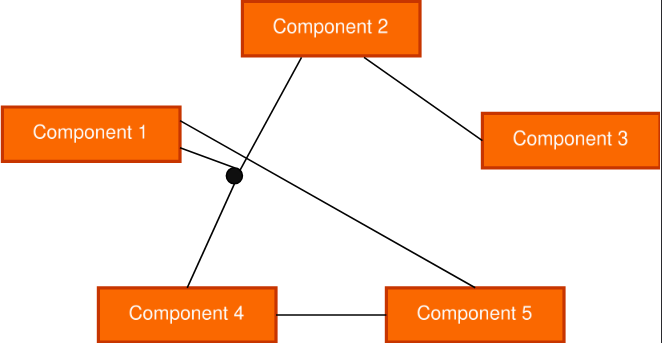
Electronic circuits can be modeled with routers replaced by hyperedges connecting all associated components
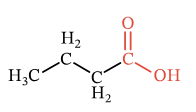
Molecules can be depicted more accurately, with functional groups like carboxylic acids joined into hyperedges to highlight their higher-order relationship

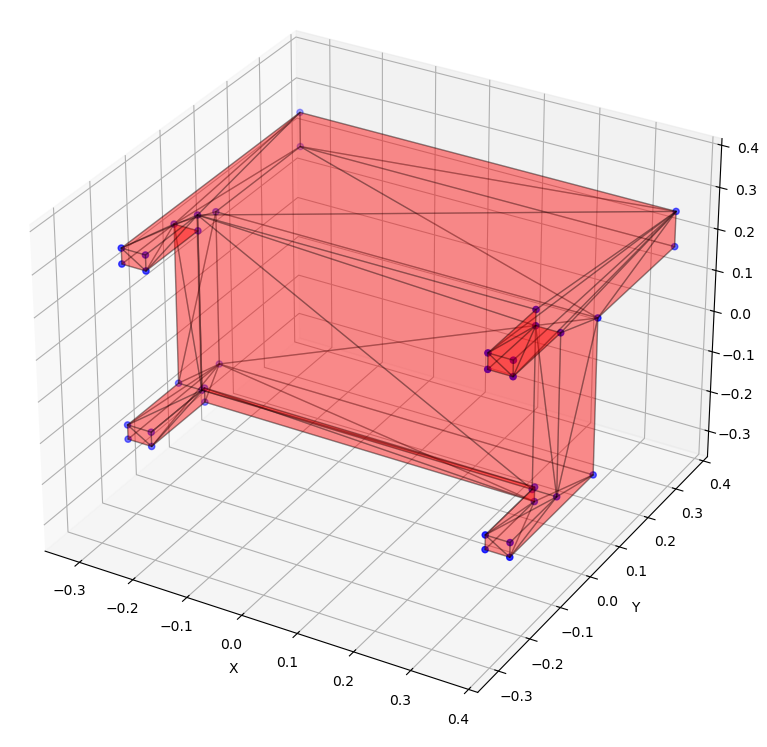
Examples of hypergraph applications

Our work aims to develop a deep-learning based method capable of generating new samples from a given distribution of hypergraphs. For instance, given examples of 3D meshes representing variants of an object, we want to train a model that can generate new instances. As an initial step, we focus solely on the underlying topology of hypergraphs, disregarding features of nodes and hyperedges.

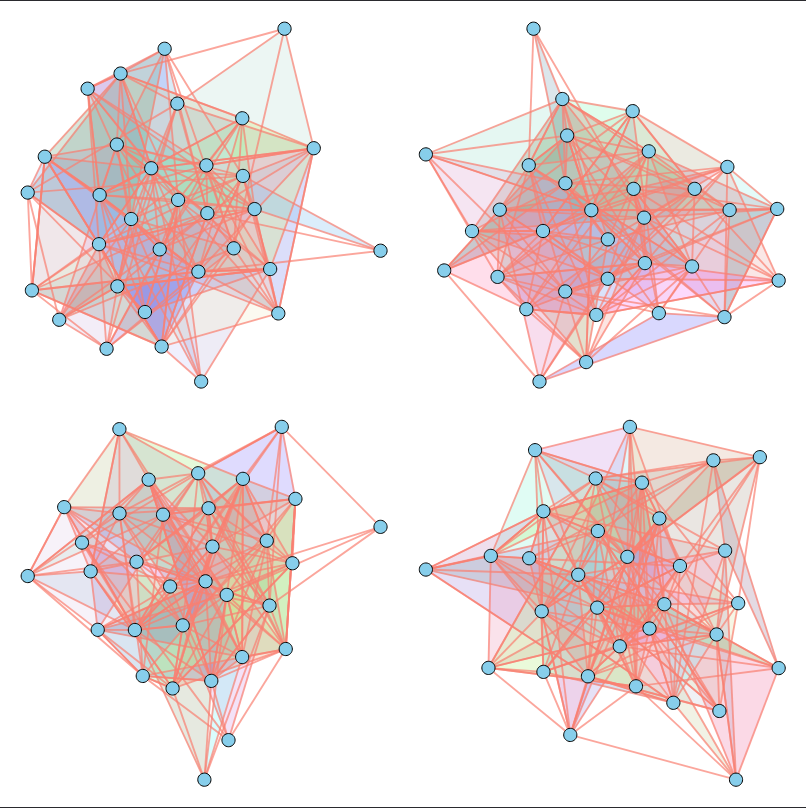
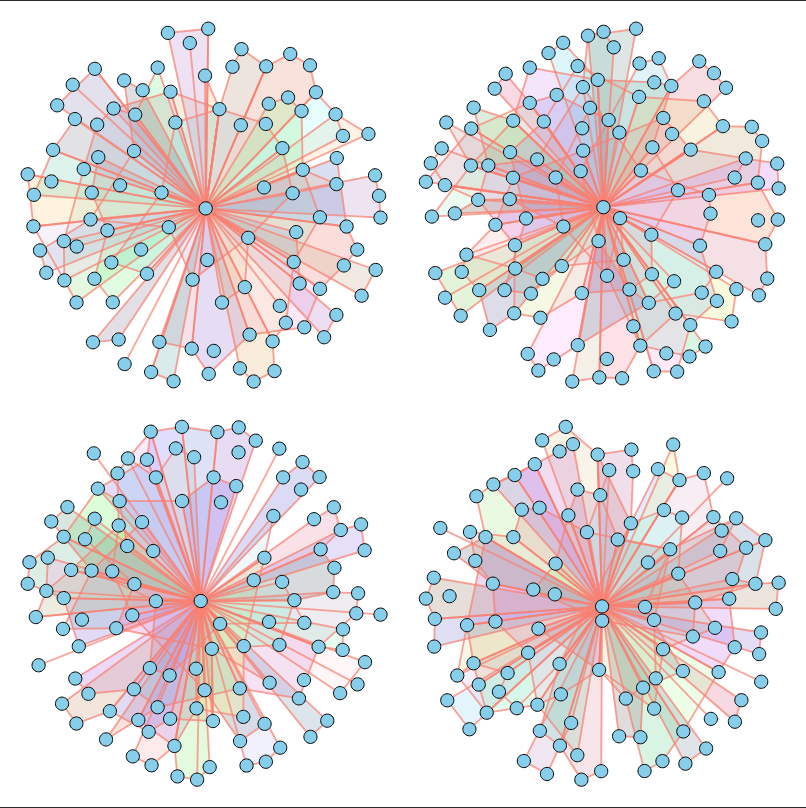
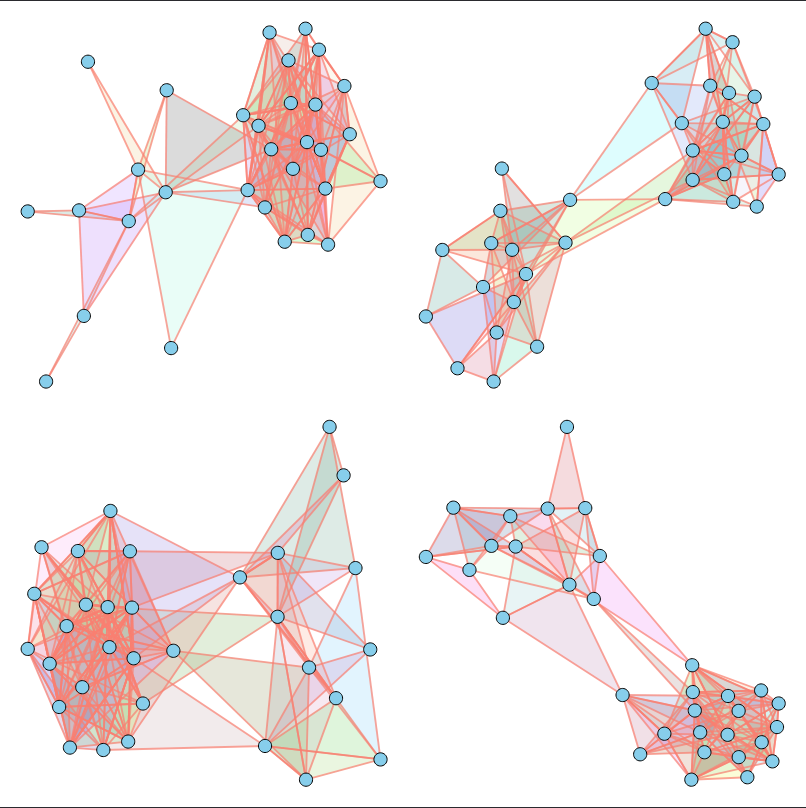
Examples of datasets we tested our method against

In other words, given a dataset of unfeatured hypergraphs (without 3D positions, component types, or other characteristics) that share similar topological properties, our goal is to train a model capable of generating new hypergraphs with matching properties.

Main Inspiration

Our work builds upon the foundation laid by the paper Efficient and Scalable Graph Generation through Iterative Local Expansion, which introduces an innovative method for graph generation. This approach draws inspiration from the tradition of graph coarsening algorithms.

When graphs become excessively large, certain algorithms may become computationally infeasible. To address this, it is possible to create smaller, representative versions of the original graph (called coarsened versions) that retain key characteristics and properties. The authors of the aforementioned paper employed a spectrum-preserving graph coarsening technique. This method merges pairs of adjacent nodes in a way that preserves a subspace of the eigenvalues and eigenvectors of the original graph, maintaining crucial structural information.

During coarsening, pairs of adjacent nodes are iteratively merged in order to create a reduced version of the graphs while preserving its spectral properties, i.e., preserving its structural information. For instance, the above coarsening sequence preserves the two-blocks structure of the graph and does not merge them until the final step.

The coarsening algorithm is applied iteratively to create a coarsening sequence. The first element in this sequence is the original graph, while the last is a fully reduced version comprising a single node. The challenge then becomes training a model to invert this coarsening process.

Starting from a step in the sequence, the model must identify which nodes result from merging at the previous step. These nodes are then duplicated and connected, with each child retaining the connections of its parent node (expansion). A second model then determines which edges should be retained in the final graph (refinement).

At each step, a first model chooses which nodes need to be duplicated before a second model filters out the resulting edges.

The generation process simply involves applying this expansion and refinement procedure iteratively until obtaining a graph of the desired size. This approach scales more efficiently compared to existing techniques, as it leverages the graph’s sparsity. When two parts of the graph become disconnected during an early generation step, there’s no need to check for connections later, significantly reducing computational overhead.

Our Work

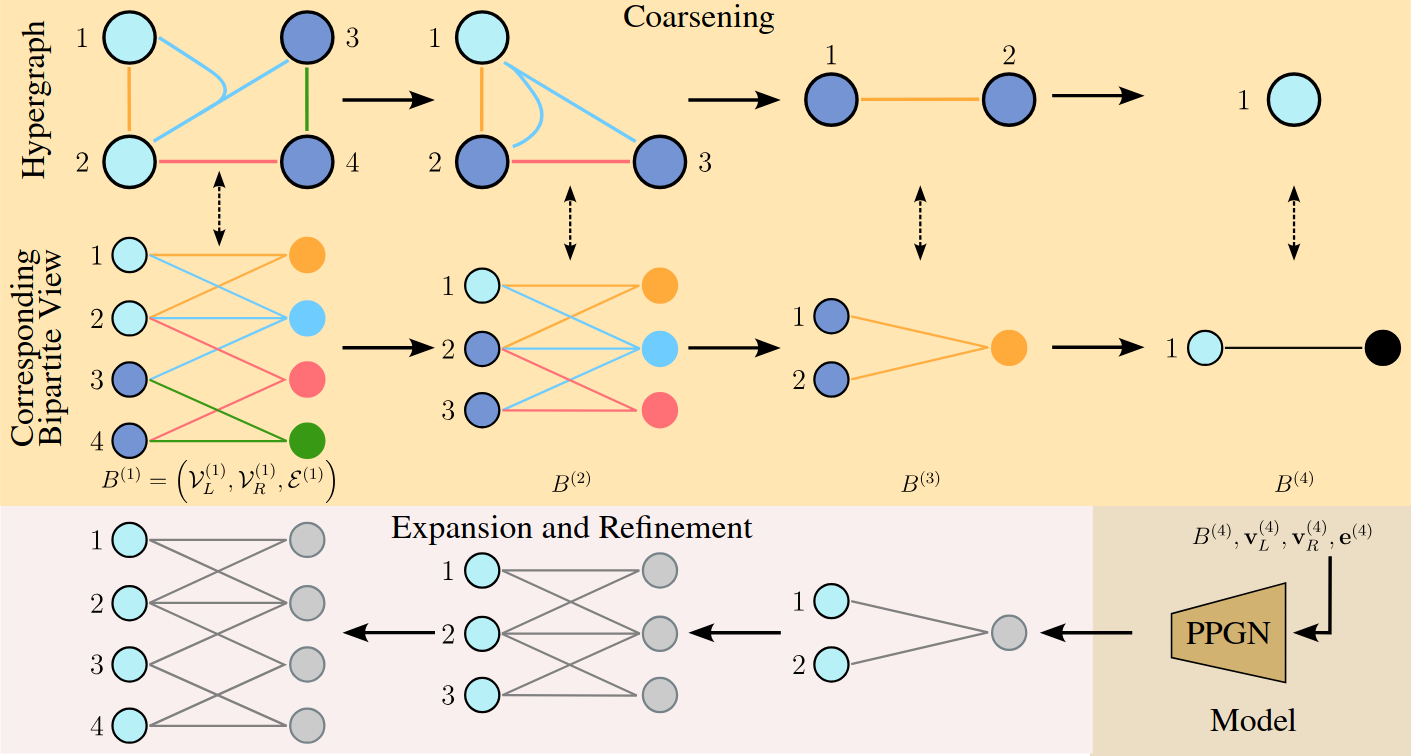
We have successfully generalized this generation method to hypergraphs and tested it on several datasets. Given the challenges of working directly with hypergraphs due to variable hyperedge sizes and complex node relationships, we project the problem back into graph space using two equivalent representations.

Coarsening Sequence / Downsampling

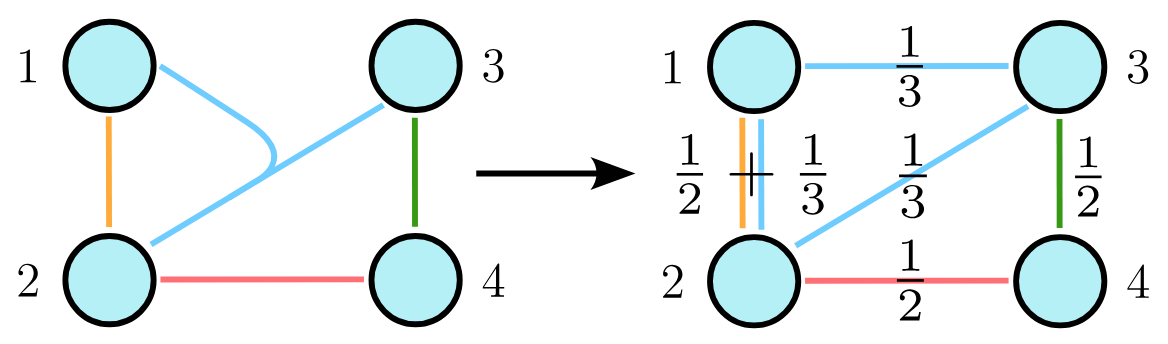
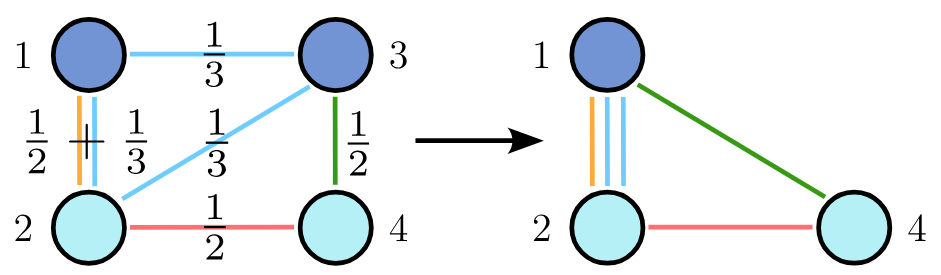
Coarsening: (a) Compute the weighted clique expansion by collapsing each hyperedge into an appropriately weighted clique. (b) Coarsen the clique expansion while preserving the spectral properties of the hypergraph (dark blue nodes).

To apply coarsening algorithms to hypergraphs, we represent them as their clique expansion. In this representation, each hyperedge \(e\) is transformed into a clique weighted by \(1/ \vert e \vert\) , where \(\vert e \vert\) is the size of the hyperedge. When an edge appears in multiple cliques, its weight becomes the sum of the weights from each clique.

This clique expansion is particularly useful for coarsening, as it maintains the same number of nodes as the original hypergraph and shares its spectral properties. Consequently, node mergings that preserve spectral properties in the clique expansion also preserve them in the hypergraph. To construct a coarsening sequence for a given hypergraph, we create an equivalent sequence for its clique expansion and merge the same pairs of nodes.

However, it’s important to note that while deriving the clique expansion from a hypergraph is straightforward, the reverse process is NP-hard, which makes it infeasible to work with the clique expansion during generation.

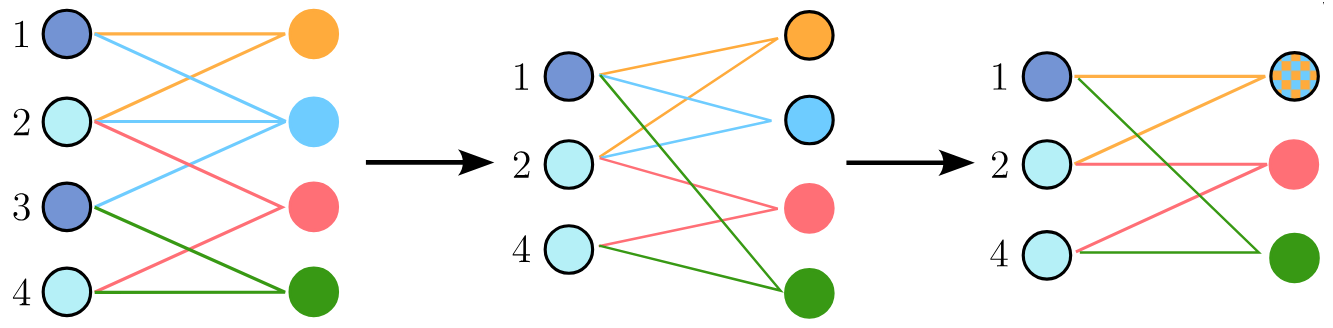
(c) Update the bipartite view: corresponding left side nodes (in dark blue) are merged, then right side nodes representing the same hyperedge (circled in black) are merged.

To address this limitation, we maintain another parallel representation of the hypergraph: the star expansion. This representation depicts the hypergraph as a bipartite graph, with one set of nodes corresponding to the hypergraph’s nodes and the other representing hyperedges. Each node is connected to the hyperedges containing it.

When nodes are merged in the clique expansion, the same nodes are merged in the star expansion. If two nodes representing hyperedges have identical connections (i.e., represent the same hyperedge), they are also merged after the node mergings in the clique expansion. Beware that in this scheme, a single pair of node mergings can result in the merging of up to three hyperedges.

Coarsening Inversion / Upsampling

Our model starts from a single pair of linked nodes (in the bipartite representation) and iteratively expands the left-side nodes (in dark blue) and right-side nodes (in red), where each duplicate keeps the connections of its parent node. Then, our method refines the resulting bipartite graph filtering edges to recover an appropriate local structure.

Beginning from a coarsening step, we train a model to identify which nodes and hyperedges result from merging at the previous coarsening step. These nodes are then expanded (nodes are duplicated twice, while hyperedges can be duplicated two or three times), with each child retaining its parent’s connections. A second model is then trained to selectively filter out regular edges, reconstructing an accurate topology. Generation starts with a single pair of connected node (the minimal bipartite graph) and iteratively applies the above scheme until obtaining a hypergraph of the desired size. Once it is attained, we can retrieve the generated hypergraph by replacing each node representing a hyperedge with a hyperedge connecting all its neighbors.

Pipeline

Combining everything gives the above pipeline: (a) A coarsening algorithm is applied to the clique expansion and generates a coarsening sequence by merging pairs of adjacent nodes. (b) A bipartite representation is maintained in parallel, where nodes representing the same hyperedge are merged. (c) A model is trained to invert the coarsening by 1. identifying which nodes are the result of a merging at the previous step and 2. filtering out the edges added during the expansion.

Results and Limitations

Results

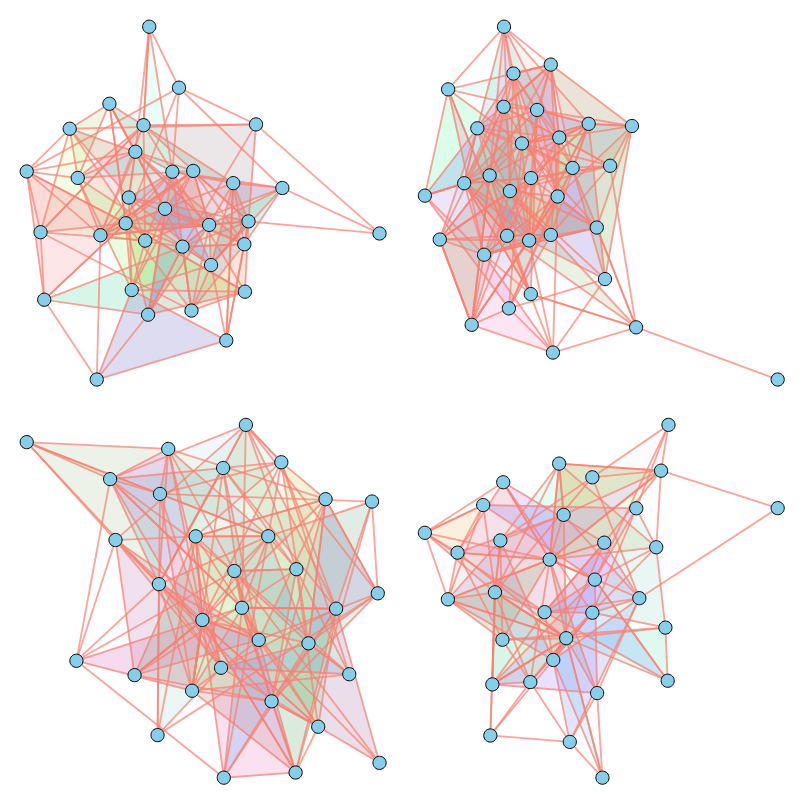
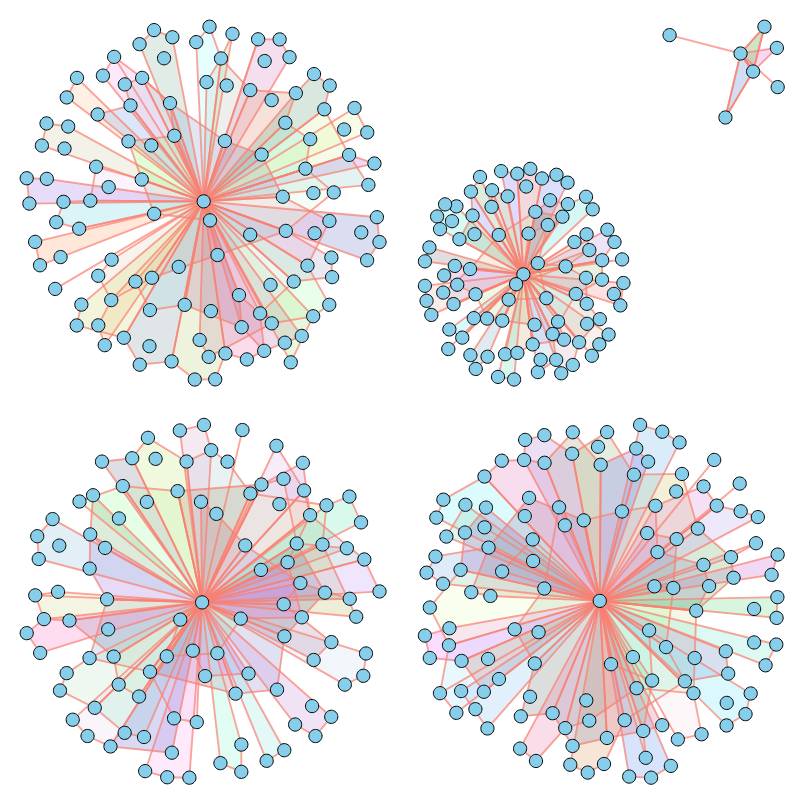
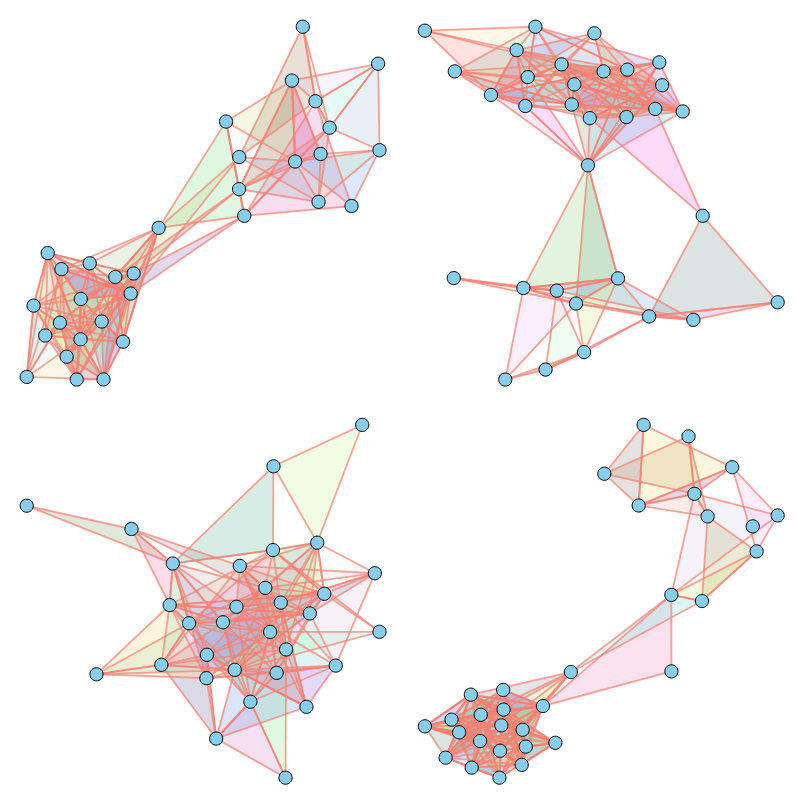
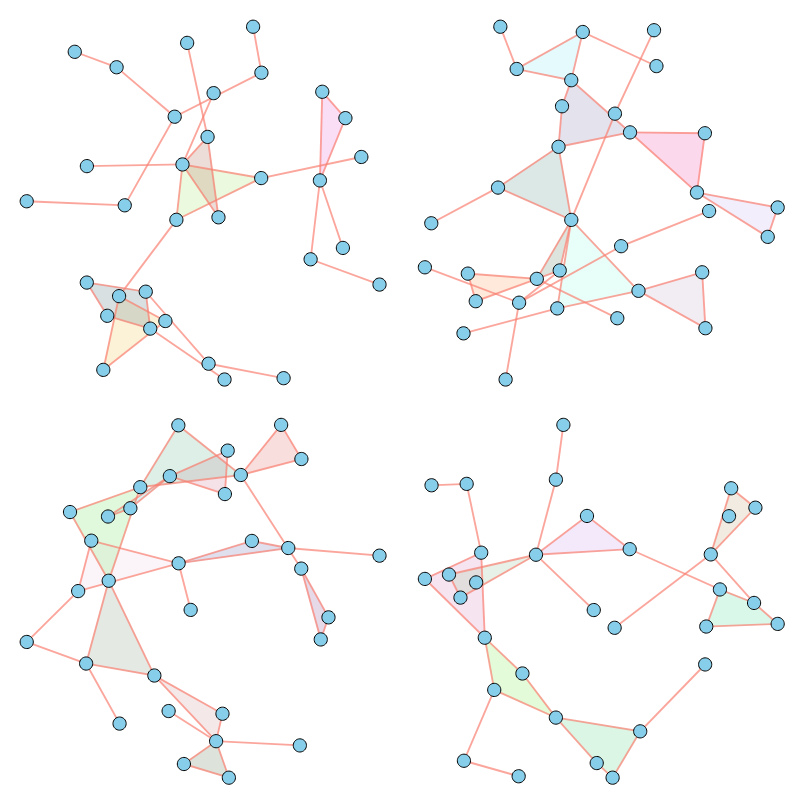
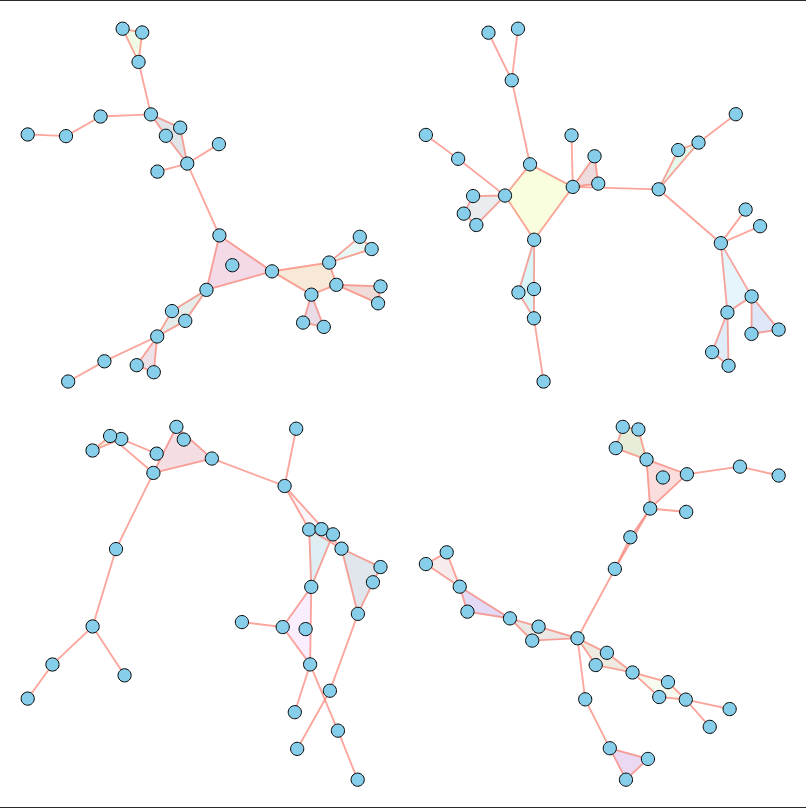
Examples of generated samples corresponding to the datasets shown at the beginning.

As illustrated above, our method successfully imitates a variety of properties. For a comprehensive analysis of numerical results across various metrics, please refer to our paper.

Limitations

Our method currently appears to disregard the specified number of nodes during generation, instead sampling from the node count distribution of the training data. Additionally, it encounters difficulties when dealing with datasets containing large hypergraphs.

Conclusion

This work represents a significant first step towards deep-learning based hypergraph generation. Our future research will focus on improving the model’s accuracy during generation, particularly concerning node count adherence, and expanding support for feature generation.

When using our work, please cite our paper:

@misc{gailhard2024hygenediffusionbasedhypergraphgeneration,
  title = {HYGENE: A Diffusion-based Hypergraph Generation Method},
  author = {Gailhard, Dorian and Tartaglione, Enzo and Naviner, Lirida and Giraldo, Jhony H.},
  year = {2024},
  eprint = {2408.16457},
  archiveprefix = {arXiv},
  primaryclass = {cs.LG},
  url = {https://arxiv.org/abs/2408.16457},
}

Acknowledgments

We acknowledge the ANR – FRANCE (French National Research Agency) for its financial support of the System On Chip Design leveraging Artificial Intelligence (SODA) project under grant ANR-23-IAS3-0004. This project has also been partially funded by the Hi!PARIS Center on Data Analytics and Artificial Intelligence.