FAHNES: Feature-aware (Hyper)graph Generation via Next-Scale Prediction

This blog post presents our paper, FAHNES: Feature-aware (Hyper)graph Generation via Next-Scale Prediction [1], which builds upon and extends our previous work, HYGENE: A Diffusion-based Hypergraph Generation Method [2].

TL;DR: We introduce a framework for generating (hyper)graphs with both node and (hyper)edge features, based on an “unzoom-zoom” approach. In the unzoom phase, the input (hyper)graph is progressively coarsened by clustering nodes and (hyper)edges, while averaging their features and tracking the size of each cluster. In the zoom phase, a model is trained to reverse this process—predicting finer-grained structure, cluster sizes, and associated features from the coarser representation. New (hyper)graphs are generated by recursively applying this zoom model, incrementally increasing detail until the desired size is reached.

In the following, we present our work for hypergraphs. It can be straightforwardly adapted to graphs by following the methodology of [3] and incorporating our new components.

Preliminaries

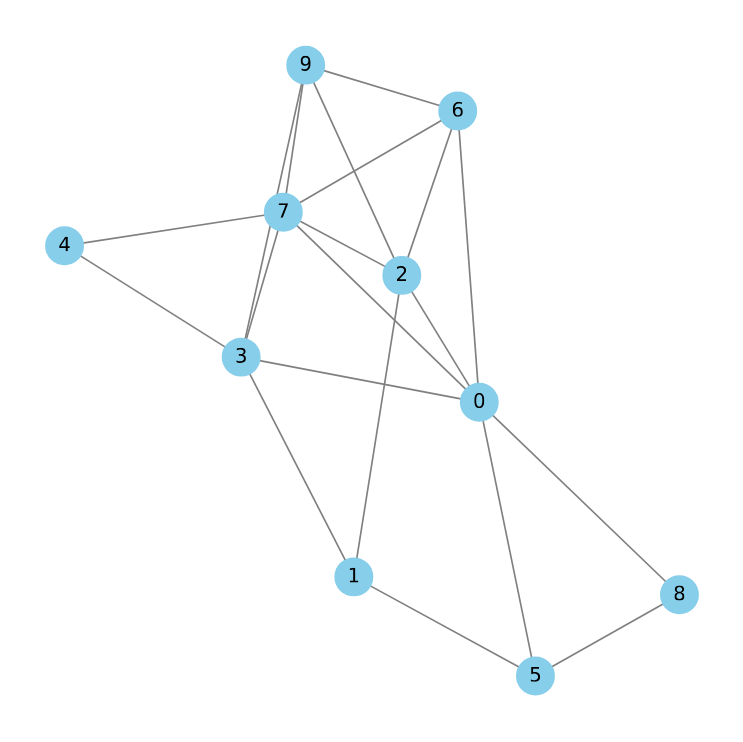
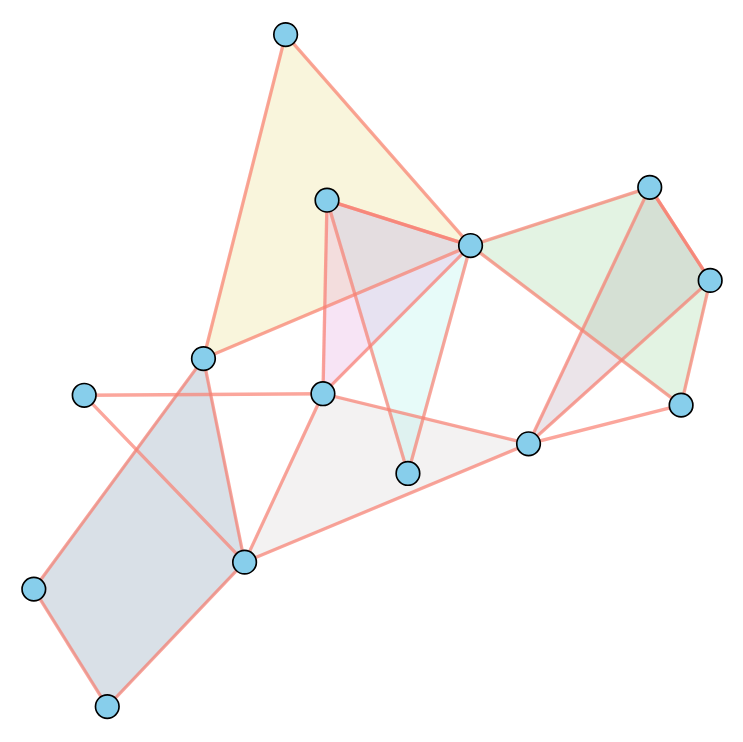
Traditional graphs consist of nodes connected by edges, where each edge links exactly two nodes. Hypergraphs, by contrast, offer a more expressive framework: their edges—called hyperedges—can connect any number of nodes simultaneously. This allows hypergraphs to capture higher-order relationships that go beyond pairwise interactions. For example:

• 3D meshes can be represented with triangles as 3-node hyperedges
• Electronic circuits can be modeled with routers replaced by hyperedges connecting all associated components
• Molecules can be described more accurately by grouping functional substructures (e.g., carboxylic acids) into hyperedges

Our goal is to develop a deep learning framework capable of generating new samples from a distribution of featured hypergraphs. For example, given a dataset of 3D meshes representing variations of an object, we aim to train a model that can generate novel, realistic instances.

While our previous work, HYGENE [2], addressed the generation of hypergraph topology, FAHNES builds upon this by improving topological quality and incorporating node and hyperedge features into the generation process. We also adress the limitations of Efficient and Scalable Graph Generation through Iterative Local Expansion [3], which introduces a hierarchical framework for graph generation, but was unable to generate features.

Example datasets used to evaluate our method. We use 3D meshes, molecular hypergraphs, and point cloud graphs as demonstrations of the capabilities of our method for both hypergraphs and graphs. Edges are omitted on point clouds for clarity.

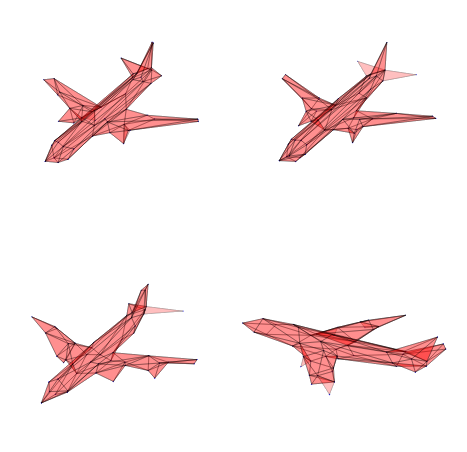
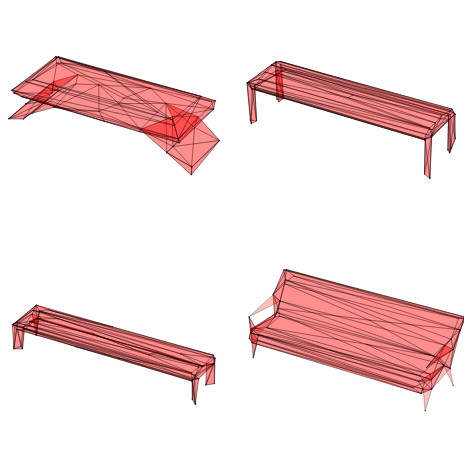
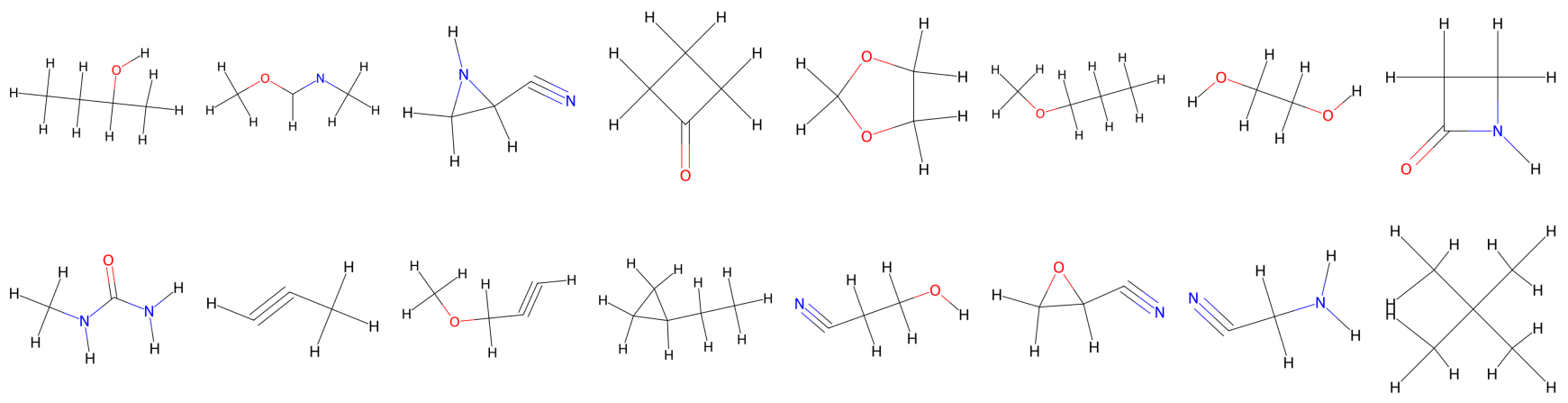
In short, given a dataset of featured (hyper)graphs—annotated with 3D positions, atom and bond types, or other attributes—our objective is to train a model that can generate new samples with similar structural and feature-based properties.

Main Inspirations

HYGENE: A Diffusion-based Hypergraph Generation Method [2]

Our method for hypergraph generation builds on our previous work HYGENE: A Diffusion-based Hypergraph Generation Method [2], which uses an “unzoom–zoom” scheme:

1. Hypergraph Downsampling (Unzoom)

To enable coarsening on hypergraphs, we project them into graph space using two complementary representations:

• Clique Expansion: Each hyperedge is replaced with a clique of edges weighted by \(1/ \vert e \vert\), where \(\vert e \vert\) is the hyperedge size. This preserves spectral properties, allowing us to apply traditional coarsening methods.

• Star Expansion (Bipartite Representation): The hypergraph is represented as a bipartite graph. One set of nodes corresponds to original hypergraph nodes, the other to hyperedges, with links connecting nodes to the hyperedges they belong to.

We apply a spectrum-preserving graph coarsening algorithm [4] to the clique expansion to produce a hierarchy of coarsened hypergraphs. The same node merges are mirrored in the bipartite representation, and hyperedges are merged when their node sets become identical (i.e., the same hyperedge appears twice).

Coarsening: (a) Compute the weighted clique expansion by collapsing each hyperedge into an appropriately weighted clique. (b) Coarsen the clique expansion while preserving the spectral properties of the hypergraph (dark blue nodes). (c) Update the bipartite representation: corresponding left side nodes (in dark blue) are merged, then right side nodes representing the same hyperedge (circled in black) are merged.

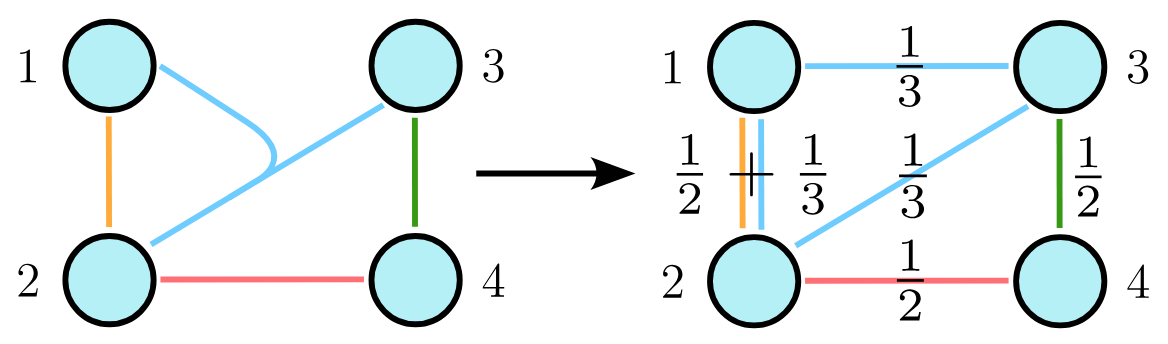
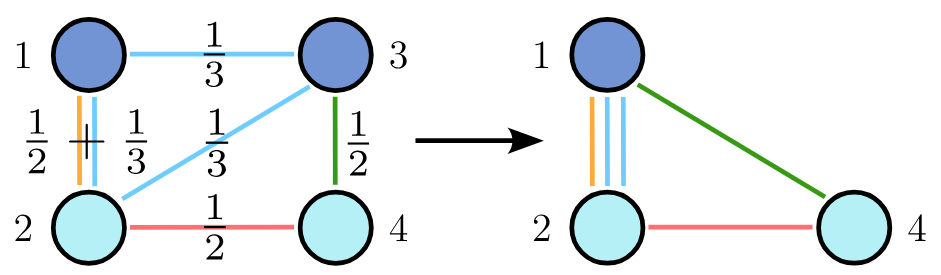
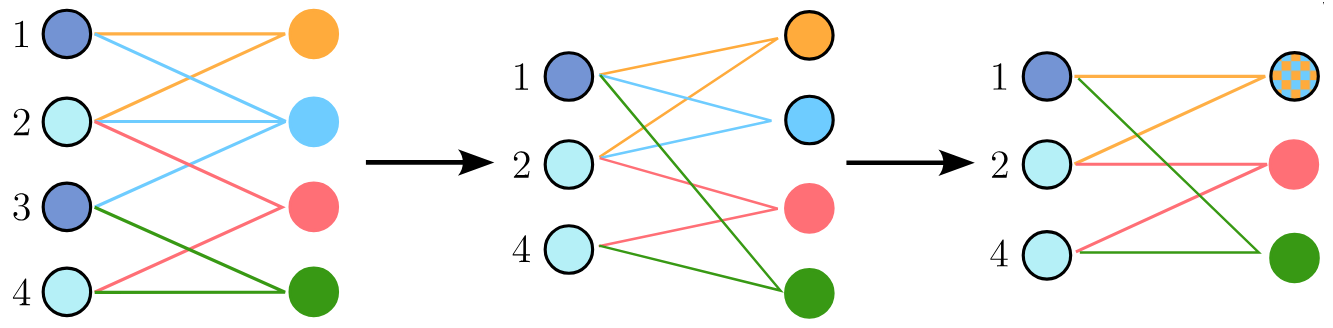
2. Hypergraph Upsampling (Zoom)

From a reduced bipartite graph, we train a neural network to reverse the coarsening process:

• Expansion: Predicts which nodes and hyperedges should be duplicated at each step. New entities inherit connections from their parent nodes/hyperedges.

• Refinement: Filters the resulting edges to ensure structural similarity.

For generation, starting with a single node and single hyperedge, we apply this expansion + refinement step iteratively to recover a full-size hypergraph.

FlowAR: Scale-wise Autoregressive Image Generation Meets Flow Matching [5]

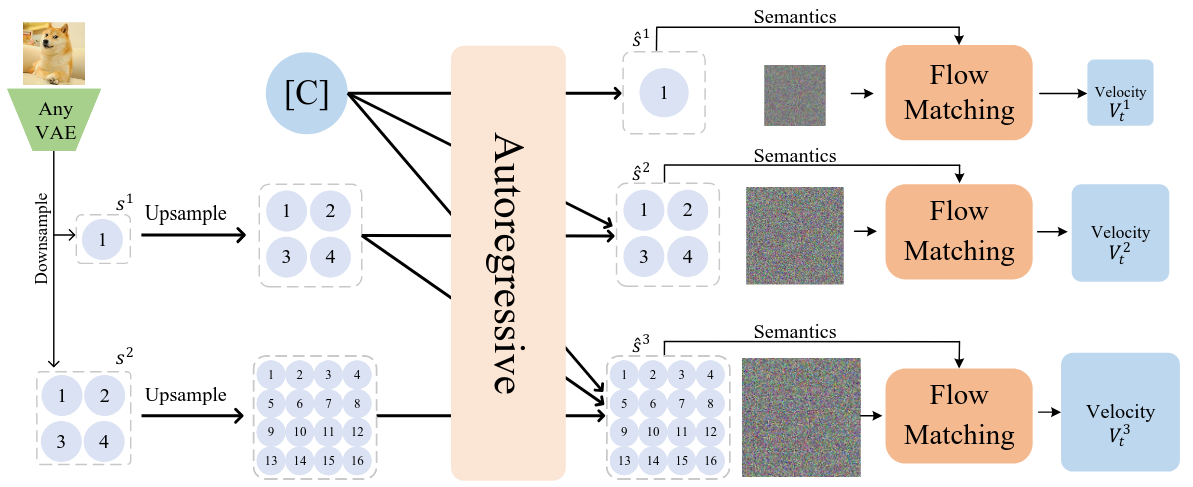
FlowAR [5] presents a hierarchical approach to image generation, where images evolve from low to high resolution through successive rounds of upsampling and denoising. At each scale, a neural network transforms Gaussian noise into a refined image, guided by an upsampled version of the previous, coarser output. This process encourages the emergence of global structure early on, while finer details are incrementally filled in—leading to both stable and coherent generation.

Inspired by this, we extend the same principle to hypergraph generation. Instead of working with pixel grids, we operate on nodes and hyperedges, treating coarseness in the hypergraph as analogous to image resolution. Each step in our model adds structural detail—introducing new nodes, hyperedges, and refining their features and connectivity. As with FlowAR, every generation stage is conditioned on the previous, coarser representation, ensuring that high-level structure guides fine-grained synthesis.

Our Work

FlowAR generates features at the pixel (node) level but cannot produce new topologies. In contrast, HYGENE can generate realistic topologies but lacks support for features. Our method, FAHNES, unifies both perspectives: it generates hypergraphs that capture both structure and attributes, supporting various modalities such as 3D meshes or molecular graphs.

The key innovations in our method include:

• A hierarchical feature generation process, in which features are predicted in a coarse-to-fine manner: at each level, children inherit an initial approximation from their parent, and the model refines these features based on the surrounding context. This not only makes feature generation tractable at large scales, but also ensures that local details remain coherent with higher-level structure.

• A node-budget mechanism, allowing us to track how many original nodes or hyperedges each coarsened entity represents. Since different parts of the hypergraph can grow at different rates, this mechanism encodes the local resolution of each region, helping synchronize and homogenize the structure overall. Beyond this, the node budget also serves as a way to explicitly mark which parts of the generated sample are already complete. This allows the model to concentrate on modifying only the unfinished regions, without learning to distinguish between finished and unfinished components.

• An adaptation of minibatch OT-coupling [6], [7] to our setting. During training, we reindex the starting noises of children within the same cluster to minimize the distance to their targets. Because graphs and hypergraphs lack a natural ordering, the learning target would otherwise be extremely noisy: all node permutations correspond to the same (hyper)graph, but loss computation requires a fixed order that may not match the predictions. Reindexing implicitly imposes a consistent order, yielding more stable targets and improving both learning speed and quality.

Coarsening Sequence / Downsampling

To enable hierarchical generation, we first construct a coarsening sequence of the input hypergraph. This process mimics the “unzoom” phase in HYGENE, but now tracks how many original nodes are represented in each node or hyperedge cluster, and incorporate features.

• Feature Averaging: When multiple nodes or hyperedges are merged, their features are averaged using their budgets as weights. This provides a coarse but representative feature vector for the cluster.

• Node/Hyperedge Budget: Initially, each node and hyperedge is assigned a budget of one, indicating it represents itself. As the hypergraph is coarsened, merged clusters inherit the sum of the budgets of their components. This budget tracks how many elements each cluster represents and will later guide the generation process.

These averaged features and budgets will later serve as inputs to the model for reconstruction.

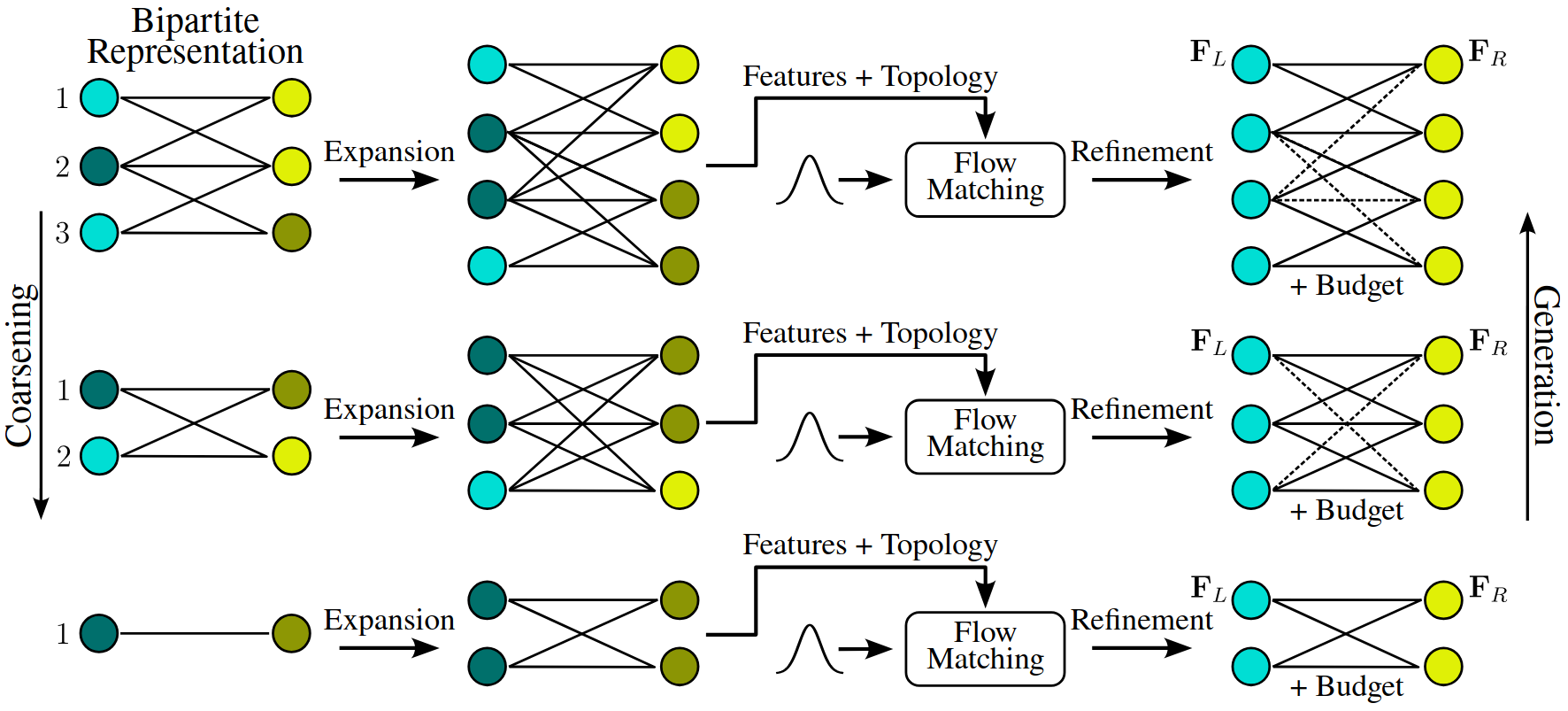
Coarsening Inversion / Upsampling

When inverting the coarsening process, feature upsampling follows a similar approach to hierarchical image generation, where coarse “pixelated” (blocky, low-resolution) representations are progressively refined to produce high-resolution images. Initially, all child nodes within a cluster inherit the same features as their parent, resulting in a coarse representation of the hypergraph. The model then refines these coarse features, progressively enhancing the details to reconstruct the full-resolution hypergraph.

Regarding node budgets, the model does not directly predict the absolute budgets for all children of a cluster. Instead, it predicts splitting ratios—the proportion of a parent’s budget allocated to each child. During training, the model learns to predict the ratio between a child’s ground-truth budget and its parent’s budget. This constrains predictions to the range \([0,1]\), which both stabilizes training (by reducing target variance) and enables diffusion directly on the simplex, yielding more robust predictions.

We further leverage the node budget mechanism to guide generation:

1. Nodes with budget = 2 that expand necessarily split their budget evenly between their two children.
2. Nodes with budget = 1 cannot expand further and are ignored during prediction, allowing the model to focus only on evolving parts of the graph.

This greatly reduces learning complexity: the model no longer needs to distinguish between “finished” and “unfinished” regions. Instead, it predicts values only for actively expanding parts. Feature refinement is similarly restricted to clusters undergoing expansion.

The figure below illustrates this strategy.

Results and Limitations

Results

Examples of generated samples corresponding to the datasets shown at the beginning.

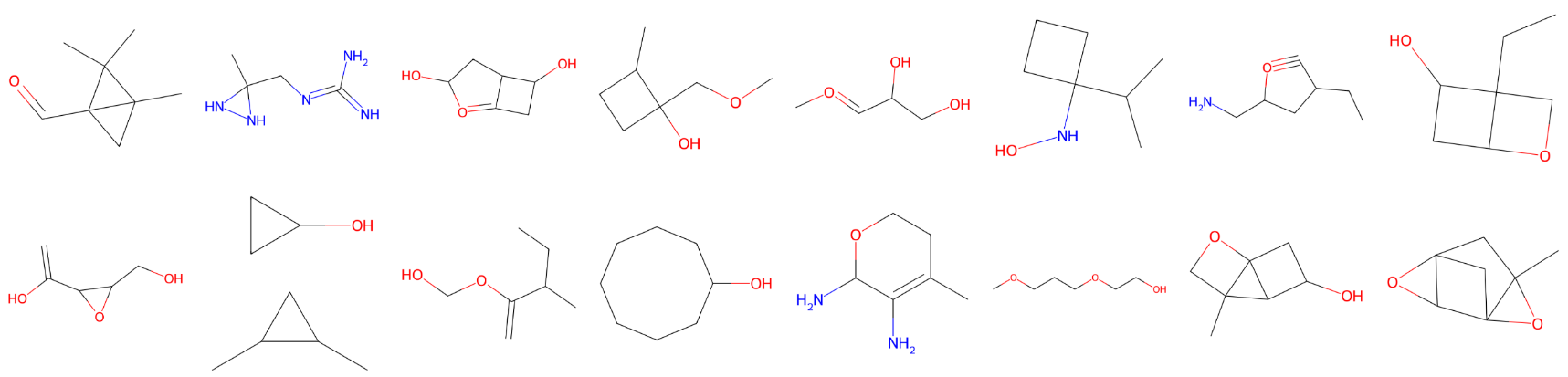
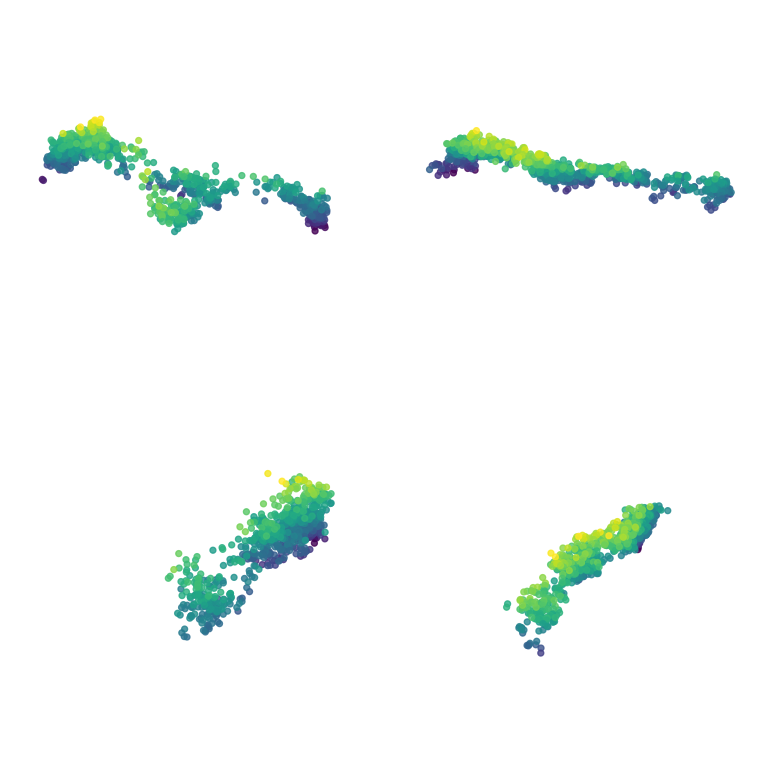
As shown above, our method can produce basic 3D meshes and point clouds, though their quality remains limited. However, it does not capture the underlying molecular rules and often generates incorrect structures. For a detailed analysis of numerical results across multiple metrics, please see our paper.

Limitations

Our experiments on molecule generation show a striking contrast with image generation. In images, hierarchical approaches often outperform simpler one-shot methods. For molecules, however, our hierarchical model currently lags behind direct one-shot graph prediction. We also found that performance is highly sensitive to hyperparameter choices, with the model being especially prone to overfitting. Interestingly, unlike image generation—where overfitting typically means reproducing the training data with high fidelity—here overfitting drastically reduces quality, tying generalization and output quality together rather than trading them off.

Conclusion

This work marks a foundational step toward hierarchical generation of featured graphs and hypergraphs. Future research will aim to improve the framework’s robustness against perturbations and prediction errors.

When using our work, please cite our paper:

@misc{gailhard2025featureawarehypergraphgenerationnextscale,
	title={Feature-aware Hypergraph Generation via Next-Scale Prediction}, 
	author={Dorian Gailhard and Enzo Tartaglione and Lirida Naviner and Jhony H. Giraldo},
	year={2025},
	eprint={2506.01467},
	archivePrefix={arXiv},
	primaryClass={cs.LG},
	url={https://arxiv.org/abs/2506.01467},
}

Acknowledgments

We acknowledge the ANR – FRANCE (French National Research Agency) for its financial support of the System On Chip Design leveraging Artificial Intelligence (SODA) project under grant ANR-23-IAS3-0004. This project has also been partially funded by the Hi!PARIS Center on Data Analytics and Artificial Intelligence.